Introduction

At 4pm ET on 2025.04.02, Trump announced sweeping tariffs on what he called "Liberation Day." Trump referred to the new levies as "discounted reciprocal tariffs," setting a unique rate for each country. There were many memeable facets to the entire spectacle – from misaligned lettering on the now-infamous Reciprocal Tariffs graphic published by the White House, to the inclusion of the McDonald Islands, a territory inhabited mostly by penguins, in the new tariff regime.

Many others have commented on these ridiculous aspects – I will focus on the math. Together, we will deep-dive how the Trump administration used math to construct a deceptive narrative and confuse the very people who will be impacted by their policy.

Here’s how the new tariffs work: The additional¹ tariff rate charged to exports from a country is simply calculated as one-half of "Tariffs Charged to the U.S.A.", which are not tariffs at all, but rather an effective rate calculated by the Trump team.

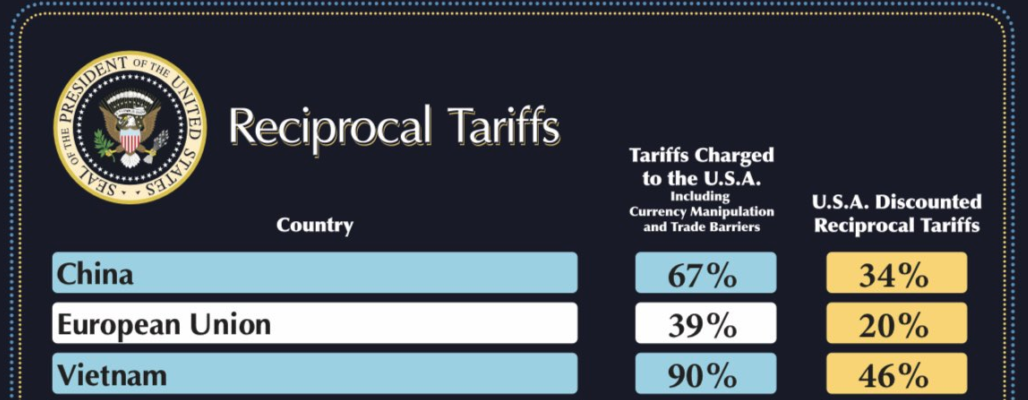
The numbers seemed arbitrary at first, but it didn’t take long for journalists and economists to work out the formula. For any country with which the U.S. has trade,

As many economists have pointed out, this is certainly not a traditional (or even valid) method to build trade models or set tariff rates. But the formula isn’t totally arbitrary – so where did it come from?

I now undertake the frustrating endeavor of making sense of the senseless. Bear in mind that my background is in finance, not economics, but lack of expertise didn’t stop the Trump administration, so it won’t stop me!

The math

Our starting point is the website of The Office of the U.S. Trade Representative (USTR). After the simplistic formula was worked out by several X.com users, in an effort to assure the public that Trump’s methods were more sophistocated, the USTR published a page called Reciprocal Tariff Calculations.

In general, the report seems to have errors², is severely lacking in context and rigor, and is poorly formatted and worded. It feels rushed and reactive.

Conveniently, the goal of the tariffs is stated at the very top:

"Reciprocal tariffs are calculated as the tariff rate necessary to balance bilateral trade deficits between the U.S. and each of our trading partners."

We’re interested in the methodology, so I will record here a verbatim copy of the section titled Basic Approach. This is a snapshot of the text as of 2025.04.04; I would hardly be surprised if the website is edited at some point in the future. It’s worth following the link above to read this for yourself to see the amaturish presentation of this world-economy-defining policy; I have replaced some of the poorly formatted text below.

In economics, this type of model is known as a Partial Equilibirum model, which describes the effects of a single action on a single market. Perhaps the most famous example of a partial equilibrium model is the law of supply and demand (and as we will see, the Trump formula is essentially a re-stating of that law). These kinds of models intentionally make many simplifying assumptions, and are thus more useful as an "intro to economics" teaching tool than as a basis for perhaps the most significant change in global trade in our lifetimes.

Before we go any further, its worth taking a beat to realize that the entire philosophy of economics represented on the USTR webpage is premised on strange and misguided beliefs about trade. Essentially, these beliefs are:

1. Trade deficits are equivalent to tariffs.

2. The U.S. should not have trade deficits.

Of course, trade deficits have nothing to do with tariffs, and our importing of coffee from countries near the equator with optimal geography for growing the crop is hardly a sign of weakness. The only way to proceed with sanity intact is to accept these false premises and then try to work out what kind of theory the authors are working with.

With that said, let’s look at some of the details. The formula incorporates the following quantities:

$\varepsilon < 0$	price elasticity of demand, set at 4
$\phi > 0$	passthrough from tariffs to import prices, set at 0.25
$m_i > 0$	total imports from country $i$
$x_i > 0$	total exports from country $i$

$x_i$ and $m_i$ were sourced from the U.S. Census Bureau for 2024, and several papers were cited for values of parameters $\phi$ and $\varepsilon$.

To arrive at their formula, I believe that the Trump team simply asked the following: What tariff, applied to a country’s imports to the U.S., would cause its imports to decrease to the exact value of U.S. exports?

There are many ways to answer this question, and it appears that the Trump team picked perhaps the simplest possible model for tariffs; something out of a 101-level economics textbook.

$\varepsilon$ is the price elasticity of import demand. Intuitively, $\varepsilon$ is simply the response in demand to a change in price. Let $Q$ be a quantity of goods, and let $P$ be the price density of those goods. In the context of trade, imports from a country is simply $Q \times P$, and $\varepsilon$ is defined as:

The great irony here is that the inclusion of $\varepsilon$ in the calculation implies that the mechanism for lowering imports is to reduce demand by raising prices for domestic consumers, something that Trump has denied will happen.

$\phi$ is the passthrough from tariffs to import prices. For example, $\phi = 0.5$ indicates that 50% of the price increase from a tariff is present in the price paid by consumers. In this context, it essentially acts as a corrective factor to the percentage change in price $\Delta P / P$. Mathematically, this is reasonable, and converts the general quantity $\varepsilon$ into one that describes tariffs. In other words,

describes the general relationship between demand and price changes, and

describes the relationship between demand and price changes resulting from a tariff.

It’s standard for economic models like this one to calibrate parameters using historical data. But again, we have a problem. Typical values for $\varepsilon$ are -0.5 to -2, and the USTR website even admits as much! From the website:

"Recent evidence suggests the elasticity is near 2 in the long run (Boehm et al., 2023), but estimates of the elasticity vary. To be conservative, studies that find higher elasticities near 3-4 (e.g., Broda and Weinstein 2006; Simonovska and Waugh 2014; Soderbery 2018) were drawn on."

In the case of Broda and Weinstein 2006, which isn’t paywalled, the paper seems to be discussing elasticity of substitution, which is not the same as elasticity of price! I might deep dive these papers at some point to see if there are any other glaring errors.

I won’t comment too much on whether or not $\phi = 0.25$ is reasonable. They claim that this value was selected based on trade with China (why doesn’t each country get its own value?), and I think 0.25 is obviously risible in many cases. If only 25% of the tariff price increases are passed onto the consumer, then the market would not have responded like it did.

It is incredibly conspicuous that $\phi = 0.25$ happens to perfectly cancel with $\varepsilon = -4$ such that $\varepsilon * \phi = -1$, which is a much more reasonable value for the effect of the tariffs. Many have speculated that the Trump team started with the barebones (imports - exports) / imports formula, and when they were criticized on their lack of sophistocation, they added two additional parameters which just so happen to cancel out in order to save face.

After studying this problem, I will give them the benefit of the doubt here, as it’s simply too lucky that their original formula would have such a convenient, yet semi-plausible variant. I do acknowledge how suspicious this is, though.

I will also grant the authors that the value of the combined parameters $\varepsilon * \phi = -1$ is a reasonable choice for the aggregate demand response of all goods to levies. The value -1 means that an increase in price from tariffs will be met with an equivalent decrease in demand. Unsurprisingly, different types of goods would have different values for this quantity, but as far as crude, back-of-the-envelope calculations go, -1 isn’t crazy.

Still, I believe a much better formulation would be something like

Again, I’m no economist, but this seems to track with more recently measured ranges of $\varepsilon$ and approximates that all import tariffs price increases are passed to the consumer.

We now have what we need to calculate the new equilibrium after a tariff. Let $V = QP$ be the total value imports before a tariff (this is $m_i$ from the Trump formula). A tariff $T$ is then imposed, resulting in a price change:

• $\Delta P = P T$ with respect to the importer

• $\Delta P = P \phi T$ with respect to the consumer

Thus,

Then we find $V'$, the total value of imported goods after the tariff with respect to the consumer.

In the graph below, we can see that $0 \le (1 - T) (1 + T) \le 1$ for all values of $T$ between 0 and 1. In other words, $V'$ will always be less than $V$, no matter the rate $T$.

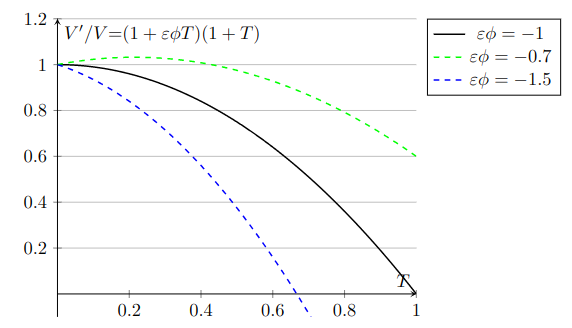
I’ve also included plots for other values of $\varepsilon \phi$ for comparison (I’m assuming $\phi$ is roughly 1, so we’re mostly concerned with $\varepsilon$). $\varepsilon \phi = -0.7$ is reasonable for less elastic goods, like food. Essential goods like medication and gas have even smaller absolute values. In this case, the total value of goods purchased by consumers may actually increase (given reasonably low tariff rates). This makes sense – most consumers will fork over the additional cash for the essentials. This net-positive import value response may also occur if exporters eat some of the cost by artificially lowering their prices. $\varepsilon \phi = -1.5$ represents elasticity for less essential items, such as luxury goods. Demand for these price-sensitive products plummets from price hikes.

Recall that our final formula, i.e. the answer to the tariff question, is

This formula differs slightly from Trump’s, but I think I figured out how to make it work. And unfortunately, to make it work, we have to think like Trump.

$V'$ is indeed the new value of the flow of goods to the consumer, but it is not the flow of money out of the country – precicely this quantity that Trump wants to decrease. Before the tariff, these were equivalent. But after the tariff, the additional $\Delta P$ is paid to the U.S. government; only $P$ is paid to the exporter!

Let $U'$ be the value paid to the exporter post tariff (before the tariff, $V = U$; this is $m_i$ in the Trump formula).

In words, the tariff $T$ which will result in a change in dollars exiting the U.S. $\Delta U$, should be $\frac{\Delta U}{\varepsilon \phi U}$. And since Trump thinks that $\Delta U$ should equal the deficit (thus making the new deficit 0), we have

Finally,

Voilà! This is the Trump formula!

Conclusion: Garbage in, garbage out

Mathematical models are wonderful tools for making sense of complex systems, but they’re only as powerful as the beliefs about the world you bake into their construction.

We’ve demonstrated that the formula published by the Trump team on the USTR website isn’t completely baseless. The point here isn’t that the math is incorrect, but rather that it’s misleading and built on faulty economics. Garbage in, garbage out.

The article posted by the Trump administration is a dishonorable and cynical use of mathematics.

They are not seeking truth or attempting to remove their bias by trusting in formulas. Their article exists to obfuscate a policy which affects everyone, to create an illusion of sophistocation and thoughtfulness where there clearly wasn’t any. It’s not just complexity for the sake of complexity, it’s complexity used as a weapon, and it is an insult to the life’s work of all of the economists who could have saved them from these mistakes.

If you would like to suggest edits or corrections, please email me at brendan.schlaman@gmail.com.